Блог вчителя математики та інформатики Синиці Олександри Сергіївни: Математичні формули

ФОРМУЛЫ АРИФМЕТИКИ:

Законы действий над числами
Некоторые математические обозначения
Признаки делимости натуральных чисел
Модуль
Действия с дробями
Пропорции
Средние величины
Некоторые конечные числовые ряды

ФОРМУЛЫ АЛГЕБРЫ:

Тождественные преобразования
Тригонометрические формулы
Прогрессии
Производная
Логарифмы
Координаты и векторы
Комбинаторика и бином Ньютона
Пределы
Интегралы

ГЕОМЕТРИЧЕСКИЕ ФОРМУЛЫ:

Планиметрия
Стереометрия

АРИФМЕТИЧЕСКИЕ ФОРМУЛЫ:
Законы действий над числами
Переместительный закон сложения: a + b = b + a.

Сочетательный закон сложения: (a + b) + с = a + (b + c).

Переместительный закон умножения: ab = ba.

Сочетательный закон умножения: (ab)с = a(bc).

Распределительный закон умножения относительно сложения: (a + b)с = aс + bс.

Распределительный закон умножения относительно вычитания: (a — b)с = aс — bс.

НЕКОТОРЫЕ МАТЕМАТИЧЕСКИЕ ОБОЗНАЧЕНИЯ И СОКРАЩЕНИЯ:

ПРИЗНАКИ ДЕЛИМОСТИ

ПРИЗНАКИ ДЕЛИМОСТИ НА «2»

Число, делящееся на «2» без остатка называется чётным, не делящееся – нечётным. Число делится на «2» без остатка, если его последняя цифра чётная (2, 4, 6, 8) или ноль

Признаки делимости на «4»

Число делится на «4» без остатка, если две последние его цифры нули или в сумме образуют число, делящееся без остатка на «4»

Признаки делимости на «8»

Число делится на «8» без остатка, если три последние его цифры нули или в сумме образуют число, делящееся без остатка на «8» (пример: 1 000 — три последние цифры «00», а при делении 1 000 на 8 получается 125; 104 — две последние цифры «12» делятся на 4, а при делении 112 на 4 получается 28; и.т.д.)

Признаки делимости на «3» и на «9»

Без остатка на «3» делятся только те числа, у которых сумма цифр делится без остатка на «3»; на «9» — только те, у которых сумма цифр делится без остатка на «9»

Признаки делимости на «5»

Без остатка на «5» делятся числа, последняя цифра которых «0» или «5»

Признаки делимости на «25»

Без остатка на «25» делятся числа, две последние цифры которых нули или в сумме образуют число, делящееся без остатка на «25» (т.е. числа, оканчивающиеся на «00», «25», «50», «75»

Признаки делимости на «10», «100» и на «1 000»

Без остатка на «10» делятся только те числа, последняя цифра которых ноль, на «100» — только те числа, у которых две последние цифры нули, на «1000» — только те числа, у которых три последние цифры нули

Признаки делимости на «11»

Без остатка на «11» делятся только те числа, у которых сумма цифр, занимающих нечётные места, либо равна сумме цифр, занимающих чётные места, либо отличается от неё на число, делящееся на «11»

АБСОЛЮТНАЯ ВЕЛИЧИНА — ФОРМУЛЫ (МОДУЛЬ)

|a| ? 0, причём |a| = 0 только если a = 0; |-a|=|a||a2|=|a|2=a2 |ab|=|a|*|b| |a/b|=|a|/|b|, причём b ? 0; |a+b|?|a|+|b| |a-b|?|a|-|b|

ФОРМУЛЫ ДЕЙСТВИЯ С ДРОБЯМИ

Формула обращения конечной десятичной дроби в рациональную дробь:

ПРОПОРЦИИ

<span «>Два равных отношения образуют пропорцию:
Основное свойство пропорции
ad = bc

Нахождение членов пропорции
Пропорции, равносильные пропорции  : Производная пропорция — следствие данной пропорции в виде
СРЕДНИЕ ВЕЛИЧИНЫ

Среднее арифметическое
Двух величин: n величин:

Среднее геометрическое (среднее пропорциональное)
  Двух величин: n величин:

Среднее квадратичное
  Двух величин: n величин:

Среднее гармоническое
  Двух величин: n величин:

НЕКОТОРЫЕ КОНЕЧНЫЕ ЧИСЛОВЫЕ РЯДЫ

ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ АЛГЕБРАИЧЕСКИХ И ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
- Свойства арифметических корней
  Для любых натуральных n и k, больших 1, и любых неотрицательных a и b верны равенства:
- МНОГОЧЛЕНЫ
Для любых a, b и c верны равенства:

Свойства числовых неравенств

1) Если a < b, то при любом c: a + с < b + с.

2) Если a < b и c > 0, то aс < bс.

3) Если a < b и c < 0, то aс > bс.

4) Если a < b, a и b одного знака, то 1/a > 1/b.

5) Если a < b и c < d, то a + с < b + d, a — d < b — c.

6) Если a < b, c < d, a > 0, b > 0, c > 0, d > 0, то ac < bd.

7) Если a < b, a > 0, b > 0, то

8) Если , то

СООТНОШЕНИЯ МЕЖДУ ТРИГОНОМЕТРИЧЕСКИМИ ФУНКЦИЯМИ ОДНОГО И ТОГО ЖЕ АРГУМЕНТА

Формулы сложения:

Формулы двойного аргумента:

ФОРМУЛЫ ТРОЙНОГО АРГУМЕНТА:

Формулы половинного аргумента:
Формулы третьей и четвертой степени:
Формулы преобразования суммы в произведение:
Формулы преобразования произведения в сумму:
Формула приведения для преобразования выражений вида
а) перед приведенной функцией ставиться тот знак, который имеет исход
ная функция;
б) функция меняется на «кофункцию», если n нечетно; функция не меняется, если n четно. (Кофункциями синуса, косинуса, тангенса и котангенса называются соответственно косинус, синус, котангенс и тангенс.) Например:

ФОРМУЛЫ НАХОЖДЕНИЯ УГЛА:

Тригонометрические уравнения

ЕДИНИЧНАЯ ОКРУЖНОСТЬ:

ФОРМУЛЫ ПРОГРЕССИИ:
- (a1 – первый член; d – разность; n – число членов; an – n-й член; Sn – сумма n первых членов):
- (b1 – первый член; q – знаменатель; n – число членов; bn – n-й член; Sn – сумма n первых членов, S – сумма бесконечной геом. прогрессии):

Производная

- - Если функция f имеет производную в точке xo, а функция g имеет производную в точке yo = f(xo), то сложная функция h(x) = g(f(x)) также имеет производную в точке xo, причем:
  - Механический смысл производной:
  - 1) v(t) = x'(t);
  - 2) a = v'(t).
  - Геометрический смысл производной:
Координаты и векторы
1. Расстояние между точками A1(x1;y1) и A2(x2;y2) находится по формуле:

2. Координаты (x;y) середины отрезка с концами A1(x1;y1) и A2(x2;y2) находится по формулам:

3. Уравнение прямой с угловым коэффициентом и начальной ординатой имеет вид:

y = kx + q.

Угловой коэффициент k представляет собой значение тангенса угла, образуемого прямой с положительным направлением оси Ox, а начальная ордината q – значение ординаты точки пересечения прямой с осью Oy.
4. Общее уравнение прямой имеет вид: ax + by + c = 0.
5. Уравнения прямых, параллельных соответственно осям Oy и Ox, имеют вид:
ax + by + c = 0.
6. Условия параллельности и перпендикулярности прямых y1=kx1+q1 и y2=kx2+q2 соответственно имеют вид:

7. Уравнения окружностей с радиусом R и с центром соответственно в точках O(0;0) и C(xo;yo) имеют вид:
8. Уравнение:
представляет собой уравнение параболы с вершиной в точке, абсцисса которой
Прямоугольная декартова система координат в пространстве
1. Расстояние между точками A1(x1;y1;z1) и A2(x2;y2;z2) находится по формуле:

2. Координаты (x;y;z) середины отрезка с концами A1(x1;y1;z1) и A2(x2;y2;z2) находятся по формулам:

3. Модуль вектора  заданного своими координатами, находится по формуле:

4. При сложении векторов их соответствующие координаты складываются, а при умножении вектора на число все его координаты умножаются на это число, т.е. справедливы формулы:

5. Единичный вектор  сонаправленный с вектором  находится по формуле:

6. Скалярным произведением  векторов называется число:

где  — угол между векторами.

7. Скалярное произведение векторов

8. Косинус угла между векторами  и  находится по формуле:
9. Необходимое и достаточное условие перпендикулярности векторов  и  имеет вид:
10. Общее уравнение плоскости, перпендикулярной вектору  имеет вид:
ax + by + cz + d = 0.
11. Уравнение плоскости, перпендикулярной вектору  и проходящей через точку (xo;yo;zo), имеет вид:
a(x — xo) + b(y — yo) + c(z — zo) = 0.
12. Уравнение сферы с центром O(0;0;0) записывается в виде:
Комбинаторика и бином Ньютона
1) Число перестановок из n элементов находится по формуле:

2) Число размещений из n элементов по m находится по формуле:

3) Число сочетаний из n элементов по m находится по формуле:

4) Справедливы следующие свойства сочетаний:

5) Формула бинома Ньютона имеет вид:

Сумма показателей чисел a и b равна n.

6) (k+1)-й член находится по формуле:

7) Число сочетаний также можно найти по треугольнику Паскаля.

Треугольник Паскаля (до n=7):

8) Сумма биномиальных коэффициентов равна 2n.

9) Чтобы найти биномиальный коэффициент следующего члена, нужно биномиальный коэффициент предыдущего члена умножить на показатель числа a и разделить на кол-во предыдущих членов.

Пределы

Теоремы о пределах

Неопределенные интегралы

Геометрия

Планиметрия

1. Произвольный треугольник:

Центр описанной окружности – точка пересечения серединных перпендикуляров. Центр вписанной окружности – точка пересечения биссектрис. (a,b,c – стороны: — противолежащие им углы; p – полупериметр; R – радиус описанной окружности; r – радиус вписанной окружности; S – площадь; ha – высота, проведенная к стороне a):
2. Прямоугольный треугольник:
Центр описанной окружности совпадает с центром гипотенузы. (a,b – катеты; c – гипотенуза; ac, bc – проекции катетов на гипотенузу):
3. Равносторонний треугольник:
Медиана = биссектрисе. OR = Or.
4. Произвольный выпуклый четырехугольник
(d1 и d2 – диагонали; – угол между ними; S — площадь):
5. Параллелограмм
(a и b – смежные стороны; – угол между ними; ha – высота, проведенная к стороне a):
6. Ромб:
В любой ромб можно вписать окружность.
7. Прямоугольник:
Около любого прямоугольника можно описать окружность.
8. Квадрат
(d – диагональ):
9. Трапеция
(a и b – основания; h – расстояние между ними; l – средняя линия):
10. Описанный многоугольник
(p – полупериметр; r – радиус вписанной окружности):
S = pr.
11. Правильный многоугольник
(an – сторона правильного n-угольника; R – радиус описанной окружности; r – радиус вписанной окружности):
12. Окружность, круг
(r — радиус; C – длина окружности; S – площадь круга):
13. Сектор
(l – длина дуги, ограничивающей сектор; — градусная мера центрального угла; — радианная мера центрального угла):

Стереометрия

1. Произвольная призма

(l – боковое ребро; P – периметр основания; S – площадь основания; H – высота; Pсеч – периметр перпендикулярного сечения; Sбок – площадь боковой поверхности; V — объем):
2. Прямая призма:
3. Прямоугольный параллелепипед
(a,b,c – его измерения; V — диагональ):
4. Куб
(a — ребро):
5. Произвольная пирамида
(S – площадь основания; H – высота; V — объем):
6. Правильная пирамида
(P – периметр основания; l – апофема; Sбок – площадь боковой поверхности):
7. Произвольная усеченная пирамида
(S1 и S1 – площади оснований; h – высота; V — объем):
8. Правильная усеченная пирамида
(P1 и P2 – периметры оснований; l – апофема; Sбок – площадь боковой поверхности):
9. Цилиндр
(R – радиус основания; H – высота; Sбок – площадь боковой поверхности; V — объем):
10. Конус
(R – радиус основания; H – высота; l – образующая; Sбок – площадь боковой поверхности; V — объем):
11. Шар, сфера
(R – радиус шара; S – площадь сферической поверхности; V — объем):
12. Шаровой сегмент
(R – радиус шара; h – высота сегмента; S – площадь сферической поверхности сегмента; V — объем):
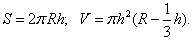
13. Шаровой сектор
(R – радиус шара; h – высота сегмента; V — объем):